La Teoria Relativa del Diner (TRM) ha establert certs paràmetres per tal que la neutralitat del Dividend Universal (DU) s’estenga en el temps i no perjudique ni beneficie unes generacions respecte de les altres. Com enraonà i establí Stéphane Laborde (l’autor de la TRM) aquests paràmetres?
En «Tirar pel dret» deia que Laborde fa alguns càlculs imaginant que l’euro muta a moneda creada pel sistema de diner-coproduït. Parteix de dades aproximades de principis de la dècada del 2010: massa monetària 10 bilions € i 330 milions de ciutadans. Simplificant, considera el nombre de ciutadans constant: el nombre dels qui entren en el sistema cada any coincideix amb el nombre dels qui l’abandonen. Els diners coproduïts l’any inicial (any 0) per a començar a rutllar el sistema és un percentatge (c) dels 10 bilions €. La qüestió és decidir un valor apropiat de c, i l’enginyer francés ho fa connectant-lo amb l’esperança de vida (ev) de l’UE, 80 anys. La decisió es basa en un procés d’aproximació i tempteig. Anem a pams.
Quan comencés a funcionar el nou sistema monetari, la massa monetària creixeria anualment segons una expressió que té la forma de l’interés compost(1), ja que els diners coproduïts equitativament cada any com a DU serien el percentatge (c) de la massa monetària assolida l’any anterior, i per tant augmenta cada any(2). Laborde ens visualitza el pas del temps mitjançant la imatge del raig d’aigua que surt per l’aixeta fins que es desfà en arribar a la basseta. El raig està format per 80 files iguals corresponents als 80 anys d’esperança de vida. Una fila es desfà en arribar a la basseta i una altra igual entra des de l’aixeta. Mentre la massa de la fila inicial arriba a la fi del seu camí, la massa total que ha eixit de l’aixeta és la de 80 files, és a dir, 80 vegades la massa d’una fila. La correspondència amb el cas del diner-coproduït no es completa, perquè en el raig d’aigua cada fila té la mateixa massa, i en el diner-coproduït de Laborde cada generació (cada fila) crea més massa (monetària) que la fila anterior, ja que la llei de creixement té la forma de l’interés compost.
Tanmateix, la imatge és útil, i Laborde l’usa per imposar la condició que la massa monetària quan han transcorregut 80 anys (una esperança de vida) siga 80 vegades la massa monetària inicial. Per tant, passats 80 anys, la massa monetària de la zona euro seria 80·(10 bilions €)= 800 bilions €. Si substituïm aquesta quantitat en la fórmula de nota (1), amb n= 80, tenim
800 bilions = 10 bilions·(1+c)80.
I resolent surt que c= 0,0563, que en percentatge és 5,63%. He preparat un gràfic (fet manualment) per a visualitzar i comentar el que anem trobant a continuació. Les dades per a construir la forma de les corbes estan preses d’un simulador de diner coproduït que podeu explorar i utilitzar: La TRM en color.
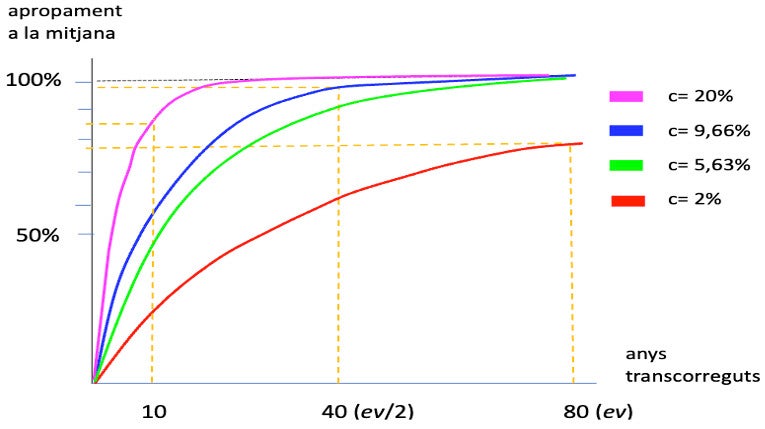
La coproducció constant i equitativa de diner provoca que la suma dels diners rebuts per un membre de la comunitat coproductora convergeix (sense arribar-hi completament) a una mitjana representada per la massa monetària dividida pel nombre de membres. Els nounats que coprodueixen el DU anual durant el primer any de vida estan lluny de la mitjana, i en passar els anys van apropant-se a ella. La taxa de creixement c determina l’extensió i el ritme d’apropament. Laborde opina que el valor c= 5,63% obtingut anteriorment, i que dona la corba verda, és el valor mínim a considerar, però no l’òptim. Expliquem açò.
En la corba verda, un individu ha coproduït el 98% de la mitjana quan fa 80 anys, i amb 40 anys hauria arribat al 88%. Laborde creu desitjable que a la meitat de l’esperança de vida (40 anys) un individu haja coproduït una quantitat més a prop de la mitjana. Repetint els càlculs anteriors, però usant 40 on abans hem usat 80, resulta c= 0,0966, que en percentatge és 9,66%, corresponent a la corba blava. En aquest cas, als 80 anys s’ha assolit el 99% de mitjana, però als 40 ja s’hauria arribat al 97%, sensiblement superior al 88%. Laborde conclou, per a ev= 80 anys, acotant el valor de c entre 5,63% i 9,66%.
Per ajudar a comprendre millor el que estem enraonant he afegit les corbes vermella i rosa. La vermella, c= 2%, mostra que en 80 anys no s’arriba al 80% de la mitjana, és a dir, que a taxes d’increment c baixes ni tan sols qui completa l’esperança de vida arriba a una coproducció plena representada per apropar-se moltíssim a la mitjana. Per això considera Laborde c= 5,63% un valor mínim. Tanmateix, valors massa grans de c beneficia massa els joves. La corba rosa c= 20%, mostra que amb 10 anys un nen ja ha coproduït més del 80% de la mitjana.
El diner-deute amb interés incrementa constantment la massa monetària, un fet que he documentat i comentat amplament en altres seccions d’aquesta sèrie. Els bancs centrals controlen l’increment amb l’instrument (entre altres) de les taxes d’interés. Amb taxes baixes, que fomenten l’endeutament, la massa monetària augmenta més de pressa, i sovint ocasiona les conegudes bombolles(3). Amb taxes altes augmenta més a poc a poc (àdhuc pot minvar), privant de diner la societat quan més li cal, en les depressions. A més, la creació de diner-deute la controla el sistema bancari de banc central, que pot (i ho fa) ocasionar beneficiaris i perjudicats. El diner-coproduït proposat per la TRM també incrementa constantment la massa monetària, però la taxa d’increment triada és constant i previsible. La creació de diner-coproduït és neutral i equitativa, i està connectada amb un paràmetre humà, l’esperança de vida.
(1) M(n) = M(0)·(1+c)n. Sent M(0) la massa monetària inicial i n els anys transcorreguts
(2) Si s’usés la fórmula de l’interés simple, els diners coproduïts cada any es calcularien sempre sobre com el percentatge c de la massa monetària inicial, i seria una quantitat constant.
(3) Vegeu, per exemple, «Similar a l’esquema Ponzi».



